The Mann-Whitney U Test
There is a dire need for film scholars to understand elementary statistics if they intend to use it to analyse film style. See here for the problems a lack of statistical education creates.
This post will illustrate the use of the Mann-Whitney U test using the median shot lengths of silent and sound Laurel and Hardy short films produced between 1928 and 1933 (see here). I will also look at effect sizes for interpreting the result of the test. Before proceeding, it is important to note that the Mann-Whitney U test goes by many different names (Wilcoxon Rank Sum test, Wilcoxon-Mann-Whitney, etc) but that these are all the same test and give the same results (although they may come in a slightly different format).
The Mann-Whitney U test
The Mann-Whitney U test is a nonparametric statistical test to determine if there is a difference between two samples by testing if one sample is stochastically superior to the other (Mann and Whitney 1947). By stochastic ordering we mean that data values from one sample (X) are more likely to assume small values than the data values from another sample (Y) and that the data values in X are less likely to assume high values than Y. If Fx(z) ≥ Fy(z) for all z, where F is the cumulative distribution function, then X is stochastically smaller than Y.
We want to find out if there is a difference between the median shot lengths of silent and sound films featuring Laurel and Hardy. The null hypothesis for our experiment is that
the two samples are stochastically equal
(Ho: Fsilent (z) = Fsound (z) for all z).
In other words, we assume that there is no difference between the samples – the median shot lengths of the silent films of Laurel and Hardy are no more likely to be greater or less than the median shot lengths of the sound films of Laurel. (See Callaert (1999) on the nonparametric hypotheses for the comparison of two samples).
In order to perform the Mann-Whitney U test we take our two samples – the median shot lengths of the silent and sound films – and we pool them together to form a single, large sample. We then order the data values from smallest to largest and assign a rank to each value. The film with the smallest median shot length has a rank 1.0, the film with second smallest median shot length has a rank of 2.0, and so on. If two or more films have a median shot length with the same value, then we give each film rank an average rank. For example, in Table 1 we see that five films have a median shot length of 3.3 seconds and that these films are 5th, 6th, 7th, 8th, and 9th in the ordered list. Adding together these ranks and dividing by the number of tied films gives us the average rank of each film: (5 + 6 + 7 + 8 + 9)/5 = 7.0.
Table 1 Rank-ordered median shot lengths of Laurel and Hardy silent (n = 12) and sound (n = 20) films
 Notice that in Table 1, the silent films (highlighted blue) tend to be at the top of the table with lower rankings than the sound films (highlighted green) that tend to be in the bottom half of the table with the higher rankings. This is a very simple way to visual the stochastic superiority of the sound films in relation to the silent films. If the two samples were stochastically equal then we would see more mixing between the two colours.
Notice that in Table 1, the silent films (highlighted blue) tend to be at the top of the table with lower rankings than the sound films (highlighted green) that tend to be in the bottom half of the table with the higher rankings. This is a very simple way to visual the stochastic superiority of the sound films in relation to the silent films. If the two samples were stochastically equal then we would see more mixing between the two colours.
Now all we need to do is to calculate the U statistic. First, we add up the ranks of the silent and sound films from Table 1:
Sum of ranks of silent films = R1 = 1.0 + 4.0 + 7.0 + 7.0 + 7.0 + 10.5 + 12.0 + 13.0 + 14.0 + 18.0 +18.0 +22.5 = 134.0
Sum of ranks of sound films = R2 = 2.0 + 3.0 + 7.0 + 7.0 + 10.5 + 18.0 + 18.0 + 18.0 + 18.0 +18.0 +22.5 +24.0 + 25.0 + 26.0 + 27.0 + 28.5 + 28.5 + 30.0 + 31.0 + 32.0 = 394.0
Next, we calculate the U statistics us the formulae:
where n1 and n2 are the size of the two samples, and R1 and R2 are the sum of ranks above. For the above data this gives us
We want the smallest of these two values of U, and the test statistic is, therefore, U = 56.0. (Note that U1 + U2 = n1 × n2 = 240).
To find out if this result is statistically significant we can compare it to a critical value for the two sample sizes: as n1 = 12 and n2 = 20, the critical value when α = 0.05, is 69.0. We reject the null hypothesis if the value of U we have calculated is less than the critical value, and as 56.0 is less than 69.0 we can reject the null hypothesis of stochastic equality in this case and conclude that there is a statistically significant difference between the median shot lengths of the silent films and those of the sound films. As the median shot lengths of the sound films tend to be larger than the median shot lengths of the silent films we can say that they are stochastically superior.
Alternatively, if our sample is large enough then U follows a normal distribution and we can calculate an asymptotic p-value using the following formulae:

For the above data, U = 56.0, μ = 120.0, and σ = 25.69. Therefore z = -2.49, and we can find the p-value from a standard normal distribution. The two-tailed p-value for this experiment is 0.013. (Note that ‘large enough’ is defined differently in different textbooks – some recommend using the z-transformation when both sample sizes are at least 20 whilst others are more generous and recommend that both sample sizes are at least 10).
If some more restrictive conditions are applied to the design of the experiment, then the Mann-Whitney U test is a test of a shift function (Y = X + Δ) for the sample medians and is an alternative to the t-test for the two-sample location problem. Compared to the t-test, the Mann-Whitney U test is slightly less efficient when the samples are large and normally distributed (ARE = 0.95), but may be substantially more efficient if the data is non-normal.
The Mann-Whitney U test should be preferred to the t-test for comparing the median shot lengths of two groups of films even if the samples are normal because the former is a test of stochastic superiority, while the latter is a test of a shift model and this is not an appropriate hypothesis for the design of our experiment. It simply doesn’t make sense to speak of the median shot length of a sound film in terms of a shift function as the median shot length of a silent film plus the impact of sound technology. You cannot take the median shot length of Steamboat Bill, Jr (X), add Δ number of seconds to it, and come up with the median shot length of Dracula (Y = X + Δ). Any such argument would be ridiculous, and only the null hypothesis of stochastic equality is meaningful in this context.
The probability of superiority
A test of statistical significance is only a test of the plausibility of the model represented by the null hypothesis. As such the Mann-Whitney U test cannot tell us how important a result is. In order to interpret the meaning of the above result we need to calculate the effect size.
A simple effect size that can be quickly calculated from the Mann-Whitney U test statistic is the probability of superiority, ρ or PS.
Think of PS in these terms:
You have two buckets – one red and one blue. In the red bucket you have 12 red balls, and on each ball is written the name of a silent Laurel and Hardy film and its median shot length. In the blue bucket you have 20 blue balls, and on each ball is written the name of a sound Laurel and Hardy film and its median shot length. You select at random one red ball and one blue ball and note down which has the larger median shot length. Replacing the balls in their respective buckets, you draw two more balls – one from each bucket – and note down which has the larger median shot length. You repeat this process again, and again, and again.
Eventually, after a large number of repetitions, you will have an estimate of the probability with which a silent films will have a median shot length greater than that of a sound film. (On Bernoulli trials see here).
The probability of superiority can be estimated without going through the above experiment: all we need to do is to divide the U statistic we got from the Mann-Whitney test by the product of the two sample sizes – PS = U/(n1 × n2). This is equal to the probability that the median shot length of a silent film (X) is greater than the median shot length of a sound film (Y) plus half the probability that the median shot length of a silent film is equal to the median shot length of a sound film: PS = Pr[X > Y] + (0.5 × Pr[X = Y]).
If the median shot lengths of all the silent films were greater than the median shot lengths of all the sound films, then the probability of randomly selecting a silent film with a median shot length greater than the median shot length of sound film is 1.0.
Conversely, if the median shot lengths of all the silent films were less than the median shot lengths of all the sound films, then the probability of randomly selecting a silent film with a median shot length greater than the median shot length of sound film is 0.0.
If the two samples overlap one another completely, then the probability of randomly selecting a silent film with a median shot length greater than the median shot length of sound film is equal to the probability of randomly selecting a silent film with a median shot length less than the median shot length of a sound film, and is equal to 0.5.
So if there is no effect PS = 0.5, and the further away PS is from 0.5 the larger the effect we have observed.
There are no hard and fast rules regarding what values of PS are ‘small,’ ‘medium,’ or ‘large.’ These terms need to be interpreted within the context of the experiment.
For the Laurel and Hardy data, we have U = 56.0, n1 = 12, and n2 = 20. Therefore, PS = 56/(12 × 20) = 56/240 = 0.2333.
Let us now compare the effect size for the Laurel and Hardy paper with the effect size from my study on the impact of sound in Hollywood in general (access the paper here). For the Laurel and Hardy data PS = 0.2333, whereas for the Hollywood data PS = 0.0558. In both studies I identified a statistically significant difference in the median shot lengths of silent and sound films, but it is clear that the effect size is larger in the case of the Hollywood films than for the Laurel and Hardy films.
The Hodges-Lehmann estimator
If we have designed our experiment to understand the impact of sound technology on shot lengths in Laurel and Hardy films around a null hypothesis of stochastic equality, then it makes no sense to subtract the sample median of the silent films from the sample median of the sound films because this implies a shift function and therefore a different experimental design and a different null hypothesis.
If we are not going to test for a classical shift model, how can we estimate the impact of sound technology on the cinema in terms of a slowing in the cutting rate?
To answer this question, we turn to the Hodges-Lehmann estimator for two samples (HLΔ), which is the median of the all the possible differences between the values on the two samples.
In Table 2, the median shot length of each of the Laurel and Hardy silent films is subtracted from the median shot length of each of the sound films. This gives us a total set of 240 differences (n1 × n2 = 12 × 20 = 240).
Table 2 Pairwise differences between the median shot lengths of Laurel and Hardy silent films (n = 12) and sound films (n = 20)
If we take the median of these 240 differences we have our estimate of the typical difference between the median shot length of a silent film and the median shot length of a sound film. Therefore, the average difference between the median shot lengths of the silent Laurel and Hardy films and the median shot lengths of the sound Laurel and Hardy films is estimated to be 0.5s (95%: 0.1, 1.1). (I won’t cover the calculation of the (Moses) confidence interval for the estimator HLΔ in this post, but for explanation see here).
The sample median of the silent films is 3.5s and for the sound films it is 3.9s, and the difference between the two is 0.4s, but as the shift function is an inappropriate design for our experiment this actually tells us nothing. Now it would appear that the difference between the two sample medians and HLΔ are approximately equal: 0.4s and 0.5s, respectively. But it is important to remember that they represent different things and have different interpretations. The difference between the sample medians represents a shift function, whereas the Hodges-Lehmann estimator is the average difference between the median shot lengths.
Note than we can calculate the Mann-Whitney U test statistic directly from the above table. If we count the number of times a silent film has a median shot length greater than that of a sound film (i.e Δ < 0, the green-highlighted numbers) and add this to half the number of times the silent and sound films have equal median shot lengths (i.e. Δ = 0, the red-highlighted numbers), then we have the Mann-Whitney U statistic that we derived above: U2 = 47 + (0.5 × 18) = 56. Equally, if we add the number of times a silent film has a median shot length less than that of sound film (i.e. Δ > 0, the blue-highlighted numbers) to half the number of times the medians are equal, then we have U1 = 175 + (0.5 × 18) = 184.
Bringing it all together
Once we have performed out hypothesis test, calculated the effect size, and estimated the effect we can present our results:
The median shot lengths of silent (n = 12, median = 3.5s [95% CI: 3.2, 3.7]) and sound (n = 20, median = 3.9s [95% CI: 3.5, 4.3]) short films featuring Laurel and Hardy produced between 1927 and 1933 were compared using a Mann-Whitney U test, with a null hypothesis of stochastic equality. The results show that there is a statistically significant but small difference of HLΔ = 0.5s (95% CI: 0.1, 1.1) between the two samples (U = 56.0, p = 0.013, PS = 0.2333).
These two sentences provide a great deal of information to the reader in a simple and economical format – we have the experimental design, the result of the test, and the practical significance of the result.
Note that at no point in conducting this test have we employed a ‘dazzling array’ of mathematical operations – in fact the most complicated thing in the while process was to find the square root in the equation for σ above and everything else was numbering items in a list, addition, subtraction, multiplication, or division.
Summary
The Mann-Whitney U test is ideally suited to our needs in comparing the impact of sound technology on film style, and has numerous advantages over the alternative statistical methods:
- it is covered in pretty much every statistics textbook you are ever likely to read
- it is a standard feature in statistical software (though you will have to check which name is used) and so you won’t even have to do the basic maths described above
- it is easy to calculate
- it is easy to interpret
- it allows us to test for stochastic superiority rather than a shift model
- it is robust against outliers
- it does not depend on the distribution of the data
- it can be used to determine an effect size (PS) that is easy to calculate and simple to understand
- we have a simple estimate of the effect (HLΔ) that is consistent with the test statistic
If you want to compare more than two groups of films, then the non-parametric k-sample test is the Kruskal-Wallis ANOVA test (see here). The Mann-Whitney U test can also be applied as post-hoc test for pairwise comparisons.
References and Links
Callaert H 1999 Nonparametric hypotheses for the two-sample location problem, Journal of Statistics Education 7 (2): www.amstat.org/publications/jse/secure/v7n2/callaert.cfm.
Mann HB and Whitney DR 1947 On a test of whether one of two random variables is stochastically larger than the other, The Annals of Mathematical Statistics 18 (1): 50-60.
The Wikipedia page for the Mann-Whitney U test can be accessed here, and the page for the Hodges-Lehman estimator is here.
For an online calculator of the Mann-Whitney U test you can visit Vassar’s page here.
For the critical values of the Mann-Whitney U test for samples sizes up to n1 = n2 = 20 and α = 0.05 or 0.01, see here.
Posted on May 12, 2011, in Cinemetrics, Film Analysis, Film History, Film Studies, Film Style, Film Technology, Hollywood, Laurel and Hardy, Silent cinema, Statistics and tagged Cinemetrics, Film Analysis, Film History, Film Studies, Film Style, Film Technology, Hollywood, Laurel and Hardy, Silent cinema, Statistics. Bookmark the permalink. 5 Comments.
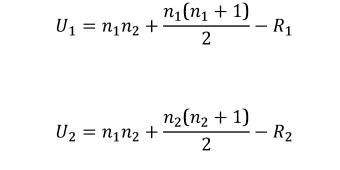


please provide the man whiyney test table for alpha level o.10 i am seeeking it
Critical values for a two-tailed test with alpha = 0.10 can be found in Table A3-9 here: http://eshare.stut.edu.tw/EshareFile/2011_4/2011_4_6c91112d.pdf
Pingback: Time Series Analysis of Top Hat (1935) « Research into film
Pingback: Machine learning literary genres from 19th century seafaring, horror and western novels | Sub-Sub Algorithm
Pingback: Machine learning literary genres from 19th century seafaring, horror and western novels | Sub-Subroutine